GranMa 2011
Oct 3 - 6, 2011
Institut Henri Poincaré, Paris
Boris Khoruzhenko, Queen Mary, University of London:
How many eigenvalues of a truncated orthogonal matrix are real?
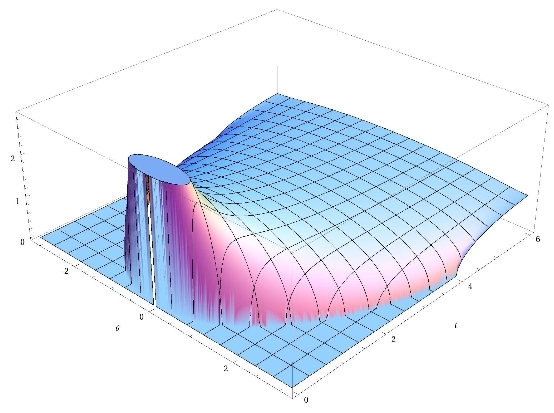
Consider a real orthogonal matrix chosen at random from the orthogonal group O(N). Truncate this matrix by removing L columns and L rows. The resulting matrix is a random contraction with eigenvalues inside the unit disk in the complex plane. We derive the joint distribution of these eigenvalues and then study their density and correlations in the complex plane in the limit of large matrix dimensions in two regimes: (i) weak non-orthogonality when L = O(1), e.g. L=1, and (ii) strong non-orthogonality when L is proportional to N, e.g. L=N/2. In the latter regime the behaviour typical of the real Ginibre ensemble is found while in the former one recovers statistics of resonance widths away from the real axis. One of the striking features of large real random matrices is the accumulation of eigenvalues on the real line. For truncated orthogonals in the regime of weak non-orthogonality we show that, on average, the total number of real eigenvalues grows logarithmically with N and their density is given by the Arctanh Law. This behaviour is similar to that of real roots of random Kac polynomials. This talk is based on a joint work with Hans-Juergen Sommers and Karol Zyczkowski.
Go to the GranMa home page.