GranMa 2011
Oct 3 - 6, 2011
Institut Henri Poincaré, Paris
Marco Bertola, :
The Painleve I transition in random matrices and in the Nonlinear Schroedinger equation: on and around the poles
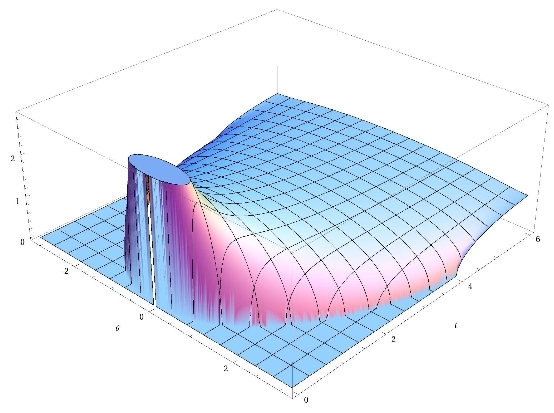
In a random matrix model with quartic potential, in the nineties it was found by Fokas, Its and Kitaev that a transition occurs that involves the first transcendent of the six Painlev\'e\ equations in the first subleading term. Later on the result was confirmed in terms of orthogonal polynomials by Duits and Kuijlaars using the nonlinear steepest descent method. The investigation stopped away from the (inevitable) poles of the particular solution to P1 involved in the asymptotic. Using a triple scaling limit we find a different universality near those poles, whereby the asymptotic is described in terms of simple rational functions and is ``nonperturbative'', meaning that the leading term is directly affected. We also investigate the "phase diagram" of the model, i.e. the separation into genus 0,1 and 2 regions. The technique of investigation at the poles of the first Painlev\'e\ transcendent can be also applied to the description of the semiclassical limit of the Nonlinear Schroedinger equation near the point of umbilic gradient catastrophe. In this case the universality has a simple "visual" interpretation, namely, the profile of the amplitude of the solution has spikes of three times the critical amplitude. This talk is based on two joint works with Alex Tovbis (UCF).
Go to the GranMa home page.