GranMa 2011
Oct 3 - 6, 2011
Institut Henri Poincaré, Paris
Gernot Akemann, Bielefeld University:
A New Two-Matrix Model and the Wilson Dirac Operator
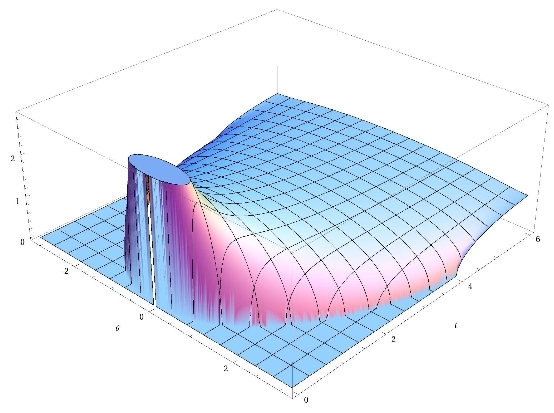
We introduce and solve a new random two-matrix model that describes the transition from the chiral Gaussian Unitary Ensemble to the Gaussian Unitary Ensemble, and generalisations thereof. The motivation for this study is to describe the effect of finite lattice spacing close to the continuum in Lattice Gauge Theory. The Hermitian version of the QCD Dirac operator discretised a la Ken Wilson is mapped to a random matrix which contains a chiral part (at zero lattice spacing) and a part that breaks this symmetry. In order to compute all its spectral correlations functions we first compute the joint probability density, given by a Pfaffian times a Vandermonde. This setting can be solved efficiently using skew-orthogonal polynomials, and we give explicit formula at finite N and in the infinite-N limit at weak non-chirality. We also discuss some open problems and relations to other models.
Go to the GranMa home page.